DDG Lecture 6

Exterior Derivative

two big ideas in calculus: differentiation vs. integration. linked by fundamental theorem of calculus.

Exterior calculus:

• differentiation of k-forms (exterior derivative)
• integration of k-forms (measure volume)
• linked by Stoke's Theorem

Goal: integrate over meshes to get discrete exterior calculus.

Motivation for exterior calculus.

Why generalize vector calculus?

• Hard to measure change in volume
• Duality clarifies distinction between different concepts/quantities.
• Topology: notion of differentiation doesn't require metric (e.g. cohomology)
• Geometry: clear language for calculus on curved surfaces.
• Physics: clear distinction between physical quantities (e.g. velocity vs. momentum)
• CS: leads directly to discretization

Exterior Derivative

Derivative as limit, slope, tangent plane, "best linear approximation".

Vector derivatives: gradient $R \rightarrow R^n$, divergence $R^n \rightarrow R$, curl $R^n \rightarrow R^n$

In coordinates:

$\phi : \mathbb{R}^n \rightarrow \mathbb{R}$

$X = u \frac{\partial}{\partial x} + v \frac{\partial}{\partial y} + w \frac{\partial}{\partial z}$ where $u,v,w : \mathbb{R^n} \rightarrow \mathbb{R}$ are coordinate functions and $\frac{\partial}{\partial x}, \frac{\partial}{\partial y}, \frac{\partial}{\partial z}$ are the basis vector fields.

defn:

grad

div

curl

The Exterior Derivative

Let $\Omega^k$ denote the space of all differential k-forms.

Unique linear map $d: \Omega^k \rightarrow \Omega^{k+1}$ such that

• differential : for k=0, $d \phi(X) = D_X \phi$
  • take the "directional derivative of $\phi$ along $X$
• product rule : $d(\alpha \wedge \beta) = d \alpha \wedge \beta + (-1)^k \alpha \wedge d \beta$
• exactness : $d \circ d = 0$

Exterior Derivative -- Differential

review: Directional Derivative

defn The directional derivative of a scalar function $\phi$ at a point $p$ with respect to a vector $X$ is the rate at which that function increases as we walk away from $p$ with velocity $X$.

This is trivially extended to $X$ vector field instead of at point $p$ by applying previous definition pointwise. The result is a scalar function.

Gradient:

i.e the gradient is the unique vector field $\nabla \phi$ whose inner product with any vector field X yields the directional derivative along X. (Note: depends on defn of inner product.)

Differential of a function

0-forms are scalar functions. Change in a scalar function can be measured via the differential. Two ways to define differential:

1. As unique 1-form such that applying any vector field gives directional derivative along those directions.

- $d\phi(X) = D_X \phi$

1. In coordinates:

- $d \phi := \frac{\partial \phi}{\partial x^1} dx^1 + \cdots + \frac{\partial \phi}{\partial x^n} dx^n$

Conceptually similar to the gradient.

grad	differential
$\left< \nabla \phi \right> = D_X \phi$	$d \phi(X) = D_X\phi$

what's the difference?

• type: vector field vs. differential 1-form
• dependence on inner product.
  • $d\phi(\cdot) = \left<\nabla \phi, \cdot \right>$
  • we have no dependence on geometry for differential.

Exterior Derivative -- Product Rule

Q: why is it true that ab = ba for a,b in R rectangle area implies commutativity.

Preduct rule of differentiation of real functions.

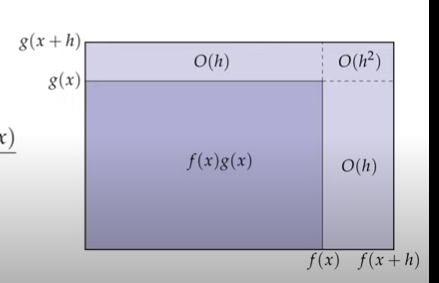
(We neglect the O(n^2) term as differentiation is linear approximation on crack.)

let $\alpha$ be a k-form and $\beta$ be an l-form. Then

Recursive evaluation of differential form

Ex. Let $\alpha := u dx, ~ \beta := v dy, ~ \gamma := w dz$ be differential 1-forms on $\mathbb{R}^n$.

where $u,v,w : \mathbb{R}^n \rightarrow \mathbb{R}$ are 0-forms. Also, let $\omega := \alpha \wedge \beta$. Then,

Note,

Therefore,

Ex. Let $\phi(x,y) := \frac{1}{2} e^{-(x^2+y^2)}$. Then

Ex. Let $\alpha(x,y) = xdx + ydy$ . Then.

Ex. Let $\alpha$ as above, then $d \star \alpha$

Exterior Derivative -- Exactness

$d \circ d = 0$

Q: let $\alpha = udx + vdy + wdz$ where $u,v,w : \mathbb{R}^3 \rightarrow \mathbb{R}$. What is $d\alpha$? A:

Vaguely reminiscent of the cross product. Thus reminiscent of curl.

Curl

Let $X := u \frac{\partial}{\partial x} + v \frac{\partial}{\partial y} + w \frac{\partial}{\partial z}$.

Then

In other words, $\nabla \times X = (\star dX^\flat)^\sharp$

Divergence

Ex. Let ambient space be $\mathbb{R}^3$. Let $\alpha$ as before. What is $d \star \alpha$?

Vaguely reminiscent to the dot product or the divergence.

i.e $\nabla \cdot X = \star (d \star X^\flat)$

Define the codifferential $\delta := \star d \star$.

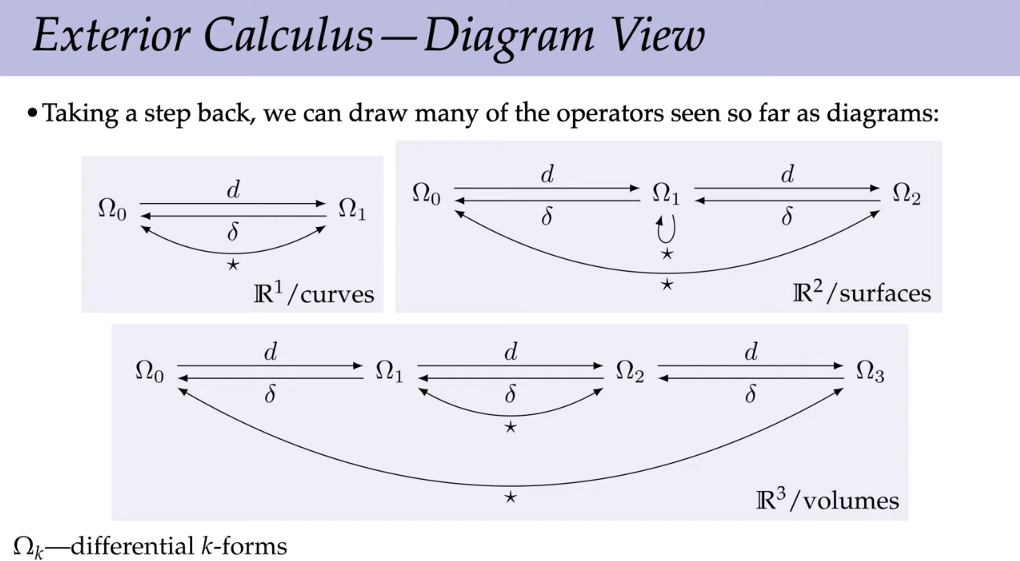
Exterior vs. Vector Derivatives

grad	div	curl
grad$\phi$	div $X$	curl $Y$
$(d\phi)^\sharp$	$\star d (\star X^\flat)$	$(\star(d Y^\flat))^\sharp$

Laplacian

$\Delta = \nabla \cdot \nabla$

or:

$\Delta = \star d \star d$

We can generalize to k-forms: