Discrete Differential Geometry 5

DDG Lecture 5

Differential Forms in Rn\mathbb{R}^n

Differential k-forms

A vector field is an assignment of vectors to each point in space.

A differential k-form is an assignment of a k-form to each point. A common abbreviation is to shorten "differential k-form" to just "k-form".

A differential 0-form is a just a scalar field. A differential 1-form is like a vector field. (But they are 1-forms at each point, so it is how to take a measurement at each point)

A differential 2-form is an area measurement at each point (x1,x2,x3).

Pointwise operations on Differential k-forms

(⋆α)p:=⋆(αp)(α∧β)p:=(αp)∧(βp)(\star \alpha)_p := \star (\alpha_p) \\ (\alpha \wedge \beta)_p := (\alpha_p) \wedge (\beta_p)

Apply operator over each k-form pointwise.

Notation: omit _p.

Differential k-forms in Coordinates

Basis Vector Fields

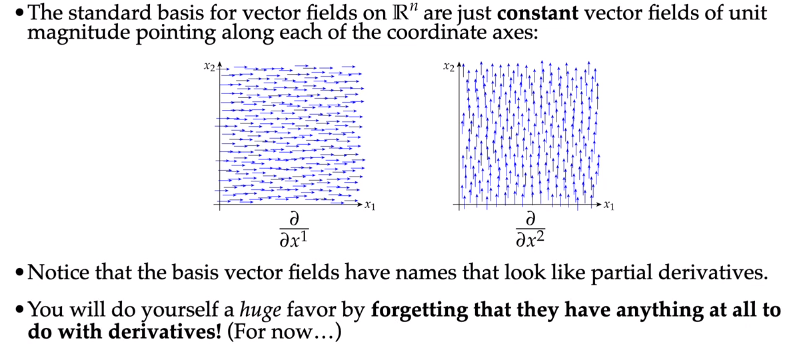
The coeffecients of the linear combination of basis fields can vary pointwise.

For differential 1-forms, call the basis 1-forms (dual bases) dx1, dx2dx^1, ~ dx^2. So α=α1dx1+α2dx2\alpha = \alpha_1 dx^1 + \alpha_2 dx^2.

dxi(∂∂xj)=δji:={1,if i=j0,otherwisedx^i \left( \frac{\partial}{\partial x_j} \right) = \delta_j^i := \begin{cases} 1, & \text{if } i = j \\ 0, & \text{otherwise} \end{cases}

Ex. Hodge star of differential 1-form.

Consider the differential 1-form: α:=(1−x)dx+xdy\alpha := (1-x)dx + x dy Q: what is the hodge star of α\alpha?

⋆α=⋆((1−x)dx)+⋆(xdy)=(1−x)(⋆dx)+x(⋆dy)=(1−x)dy−xdx\begin{aligned} \star \alpha &= \star ((1-x)dx) + \star (xdy) \\ &= (1-x)(\star dx) + x (\star dy) \\ &= (1-x)dy - x dx \end{aligned}

Ex. wedge of two 1-forms.

α:=xdx,β:=(1−x)dx+(1−y)dy\alpha := xdx, \quad \beta := (1-x)dx + (1-y)dy

α∧β=xdx∧((1−x)dx+(1−y)dy)=xdx∧(1−x)dx+xdx∧(1−y)dy=x(1−x)(dx∧dx)+x(1−y)(dx∧dy)=(x−xy)(dx∧dy)\begin{aligned} \alpha \wedge \beta &= xdx \wedge ((1-x)dx + (1-y)dy) \\ &= xdx \wedge (1-x)dx + xdx \wedge (1-y)dy \\ &= x(1-x) (dx \wedge dx) + x(1-y) (dx \wedge dy) \\ &= (x-xy) (dx \wedge dy) \end{aligned}

Note that in R2\mathbb{R}^2 all wedges of 1-forms are scalar multiples of dx∧dydx \wedge dy. The same information is contained in the hodge star.

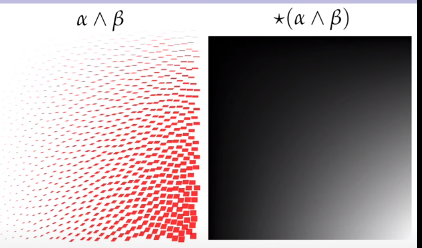
⋆(α∧β)=(x−xy)\star (\alpha \wedge \beta) = (x-xy)

Ex. Applying a Differential 1-form to a vector field

α:=xdxX:=(1−x)∂∂x+(1−y)∂∂y\alpha := xdx \\ X := (1-x)\frac{\partial}{\partial x} + (1-y)\frac{\partial}{\partial y}

apply α\alpha to XX.

α(X)=(xdx)((1−x)∂∂x+(1−y)∂∂y)=(x(1−x))(dx∂∂x)+(x(1−y))(dx∂∂y)=x−x2\begin{aligned} \alpha(X) &= (xdx) \left( (1-x)\frac{\partial}{\partial x} + (1-y)\frac{\partial}{\partial y} \right) \\ &= (x(1-x)) \left( dx \frac{\partial}{\partial x} \right) + (x(1-y)) \left( dx \frac{\partial}{\partial y} \right) \\ &= x-x^2 \end{aligned}