Discrete Differential Geometry 3

DDG Week 3

Exterior Calculus

Why?

  • Talk about signed volume
  • Geometry -> Algebraic Geometry
  • Geometric algebra (Clifford algebra, spin physics)
  • Physics
    • massless quantitiies are vectors
    • massive quantities are forms

discrete exterior calculus (DEC)

Work from linear algebra and vector calculus to Exterior Algebra and Exterior Calculus.

DEC -> Discretize all the above.

motivation: do cool stuff like solve PDEs on meshes.

Concepts:

  • Poisson
  • Helmholtz-Hodge
  • homology
  • cohomology

Applications:

  • smoothing
  • distance
  • vector field
  • parameterization
  • meshing

Wedge Product

span: the subspace that is a linear combination of the vectors.

Defn: In a vector space VV, the span of a finite set of vectors {v1,…,vk}\{v_1,\dots,v_k\} is the set of all linear combinations:

span({v1,…,vk}):={x∈V∣x=∑i=1kaivi, ai∈R}\text{span}(\{v_1,\dots,v_k\}) := \{x \in V | x = \sum_{i=1}^{k} a_i v_i, ~ a_i \in \mathbb{R}\}

Wedge product:

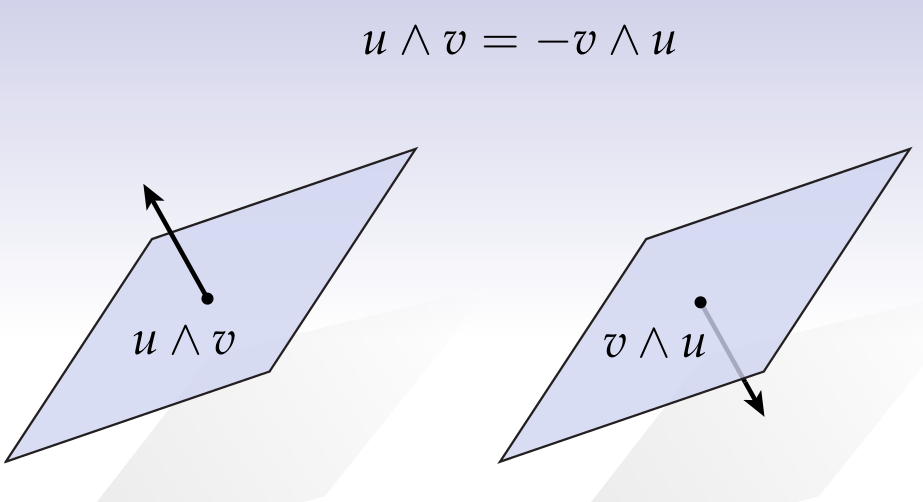
Oriented finite extent. Anti-symmetric.

note: u∧u=0u \wedge u = 0

u∧v∧w=(u∧v)∧w=u∧(v∧w)u∧(v1+v2)=u∧v1+u∧v2u \wedge v \wedge w = (u \wedge v) \wedge w = u \wedge (v \wedge w) \\ u \wedge (v_1 + v_2) = u \wedge v_1 + u \wedge v_2 \\

The resulting object is a k-vector.

  • 0-vector ?
  • 1-vector uu
  • 2-vector u∧vu \wedge v -> parallelogram (direction + magnitude)
  • 3-vector u∧v∧wu \wedge v \wedge w -> volume + direction?

A k-vector with the same area and orientation is equivalent. Any "patch" with the same area and normal is equivalent.

For convenience, say a 0-vector is a scalar.

Hodge Star

Orthogonal Compliment:

V:=span({u,v})V⊥:={x∈Rn∣<x,w>=0 ∀w∈V}V := \text{span}(\{u,v\}) \\ V^{\perp} := \{x \in \mathbb{R}^n | <x,w> = 0 ~ \forall w \in V\}

Defn Let U⊂VU \subset V be a linear subspace of a vector space VV with an inner product <⋅,⋅><\cdot, \cdot>. The orthogonal compliment of UU is the collection of vectors.

U⊥:={v∈V∣<v,u>=0 ∀u∈U}U^{\perp} := \{v \in V | <v,u> = 0 ~ \forall u \in U\}

With a compliment, we can say things like "X except Y".

⋆(u∧v)=w\star (u \wedge v) = w

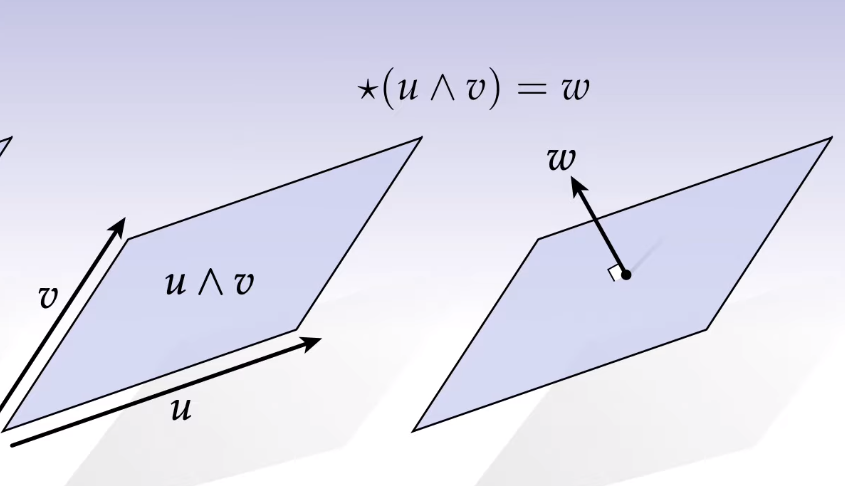
convention: z∧⋆zz \wedge \star z is positively oriented.

The 2-form is the "oriented planar segment" whereas the hodge star of a 2-vector gives us the normal to the surface (in R3\mathbb{R}^3).

Coordinate Representation

Like the basis of linear algebra, we can find the basis of VV by thinking of the wedges:

e.g. in R4B={e1,e2,e3,e4}\mathbb{R}^4 \quad \mathcal{B} = \{e_1,e_2,e_3,e_4\}

e1∧e2e1∧e3e2∧e3e1∧e4e2∧e4e3∧e4e_1 \wedge e_2 \\ e_1 \wedge e_3 \quad e_2 \wedge e_3 \\ e_1 \wedge e_4 \quad e_2 \wedge e_4 \quad e_3 \wedge e_4

The wedges e2∧e1=e1∧e2e_2 \wedge e_1 = e_1 \wedge e_2 are omitted, so in general only ei∧eji<je_i \wedge e_j \quad i < j are considered. Also, with 3-vectors we have:

e1∧e2∧e3e1∧e2∧e3e1∧e3∧e4e2∧e3∧e4e_1 \wedge e_2 \wedge e_3 \\ e_1 \wedge e_2 \wedge e_3 \\ e_1 \wedge e_3 \wedge e_4 \\ e_2 \wedge e_3 \wedge e_4

so the same general rule applies where we take all permutations such that i<j<ki < j < k. We get dim(V) choose k\text{dim}(V) ~ \text{choose} ~ k basis k-vectors for a vector space VV.