Discrete Differential Geometry Week 2

2A What is a Mesh

Mesh = Simplicial Complex.

• Abstract vs. Geometric
• Oriented, Manifold Simplicial Complex.
• Cell Complex
  • Poincare Dual
• Data structures
  • adjacency list
  • incidence matrix
  • half edge

Mesh / Topological Space (Discrete/Cont.)

Convex Set

ex. star, triangle, bottle, dodecahedron

Defn A subset $S \subset \mathbb{R}^n$ is convex if for every pair of points $p,q \in S$ the line segment between $p$ and $q$ is contained in $S$

Convex Hull

Defn For any subset $S \subset \mathbb{R}^n$ its convex hull conv(S) is the smallest convex set containing $S$, or equivalently, the intersection of all convex sets containing $S$.

ex. The convex hull of $S := \{(\pm 1, \pm 1,\pm 1) \} \subset \mathbb{R}^3$ is a cube with vertices S.

Simplex

Roughly speaking, a k-simplex is a point, a line segment, a triangle, a tetrahedron, ...

The shape defined by k+1 vertices.

Defn A collection of vectors $v_1, \dots, v_n$ is linearly independent if no vector can be expressed as a linear combination of others. i.e There is no collection of $a_1, \dots, a_n \in \mathbb{R}$ such that $v_j = \sum_{i \neq j} a_i v_i$ for any j.

Defn A collection of points $p_0, \dots, p_k$ are affinely independent if the vectors $v_i := p_i - p_0$ are linearly independent.

Defn a k-simplex is the convex hull of k+1 affinely independent points, which we call its vertices.

Note: A 2-simplex can exist in a vector space V of dim(V) > 2, or in general a k-simplex can only exist in a vector space of dimensionality at least k.

Barycentric coordinates

Any point $p$ in a k-simplex $\sigma$ can be expressed as a weighted combination of vertices, where the weights sum to 1.

$\sigma = \{\sum_{i=0}^{k} t_i p_i | \sum_{i=0}^kt_i = 1, t_i \geq 0 \forall i\}$

Also called a convex combination.

ex. The standard n-simplex is the collection of points:

$\sigma := \{(x_0, \dots, x_n) \in \mathbb{R}^{n+1} | \sum_{i=1}^n x_i = 1, x_i \geq 0 \forall i\}$

also known as the "probability simplex"

Simplicial Complex

Roughly speaking, a simplicial complex is a "A bunch of simplices".

Defn A face of a simplex $\sigma$ is any simplex whose vertices are a subset of the vertices of $\sigma$.

e.g. The faces of a triangle include the edges, vertices, and the triangle itself. The empty is set is also a face.

Defn A (geometric) simplicial complex is a collection of simplices where:

• The intersection of any two simplices is a simplex
• Every face of every simplex in the complex is also in the complex.

Defn Let $S$ be a collection of sets. If for each $\sigma \in S$ all subsets of $\sigma$ are contained in $S$, then $S$ is an abstract simplicial complex. A set $\sigma \in S$ of size k+1 is an (abstract) simplex.

This is a looser restriction than the geometric definition and not equivalent.

ex. Any undirected graph is a simplicial 1-complex.

Application: Topological Data Analysis

Try to understand data in terms of connectivity instead of geometry.

ex. Persistent Homology Start with a collection of points, grow "balls" around each point. Connect (k+1) overlapping balls into k-simplex. Track birth and death of features like connected components, holes, etc. Features that persist for a long time are likely "real".

Anatomy of a Simplicial Complex

Closure: smallest simplicial complex containing a given set of simplices. Star: Union of simplices containing a given subset of simplices. Link: Closure of the star minus the star of the closure.

Notation: For 1-complexes write $G = (V,E)$ For 2-complexes (triangle meshes) we often write $K = (V,E,F)$ where F is a triangle not to be confused with the face above.

Oriented Simplicial Complex

Basic idea: Does a 1-simplex {a,b} go from $a \rightarrow b$ or $b \rightarrow a$? Instead of an unordered set {a,b}, use an ordered tuple (a,b) or (b,a) Important for calculating integrals.

For a 2-simplex, orientation given by "winding order" of vertices. (a,b,c) != (a,c,b) (a,b,c) = (b,c,a) = (c,a,b) (a,c,b) = (c,b,a) = (b,a,c) The equivalence class of 3-tuples where tuples are equivalent if they are related by a circular shift.

Defn An oriented k-simplex is an ordered tuple, up to even permutation.

Hence, always 2 orientations*: odd, or even permutations. Convention: $(0, \dots, k)$ is positive, otherwise negative orientation.

*An oriented 0-simplex is always positively oriented.

Oriented Simplicial Complex

Defn An orientation of a simplex is an ordering of its vertices up to even permutation; one can specify an oriented simplex via one of its representative ordered tuples. An oriented simplicial complex is a simplicial complex where each simplex is given an ordering.

Defn Two distinct oriented simplices have the same relative orientation if the two (maximal) faces in their intersection have opposite orientation.

Note: Thinking about a strip from the round face of a cyllinder, a triangulation should have the same relative orientation, whereas a triangulation of the mobius strip would have an inconsistent relative orientation along one of its 2-simplices.

2B Introduction to Manifolds

Very rough idea: manifolds are a notion of "nice" space in geometry.

Key idea: a manifold locally appears like $\mathbb{R}^n$

Simplicial Manifold

Defn A simplicial k-complex is manifold if the link of every vertex looks like a (k-1)-dimensional sphere.

Aside: How hard would it be to check if a given simplicial complex is manifold? k=1 -> is the complex just a collection of closed loops? k=2 -> is the link of every vertex a closed loop? k=3 -> is each link a 2-sphere? Just check $V-E+F = 2$ (Euler's formula) k=4 -> is each link a 3-sphere? It's known to be NP

ex. Manifold triangle mesh. (k=2) -> Every edge is contained in exactly two triangles, or just one along the boundary. &&-> every vertex must be contained in a single "loop" of triangles. Or a single "fan" along the boundary.

Why is a manifold mesh desirable? By analogy: 2D-images.

• A regular grid does everything we desire.
• Very simple -> always has 4 neighbors.

Manifold meshes are similar. Manifold meshes do most things we desire. Very simple -> (predictable neighborhoods) leads to nice data structures

Topological Data Structures

Adjacency List

Store only top-dimensional simplices. ex. "hollow tetrahedron" (vertices 0,1,2,3) 0 2 1 0 3 2 3 0 1 3 1 2

Pros: simple, small storage cost Cons: hard to iterate over, e.g. edges. expensive to access neighbors. (e.g. "List of all edges touching a vertex")

Incidence Matrix

$E_0$ has rows of edges, columns of vertices. $E_1$ rows are triangles, columns are edges.

Defn Let $K$ be a simplicial complex, let $n_k$ denote the number of k-simplices in $K$, and suppose for each $k$ we give the k-simplices a canonical ordering so that they can be specified via indices $1, \dots, n_k$. The kth incidence matrix is then a $n_{k+1} \times n_k$ matrix $E^k$ with entries $E_{ij}^k = 1$ if the jth k-simplex is contained in the ith (k+1)-simplex and 0 otherwise.

Aside: complexity. Not useful if using dense matrix. Useful to have sparse data structure.

e.g

[[4 2 0]
 [0 0 3]
 [0 7 0]]

• map<(row,col), val> is useful for lookup/set. Bad for matrix multiplication.
• vector<linkedlist<(col,val)>> where vec[row]
• "Compressed column format"
  • values: [4,2,7,3]
  • row indices: [0,0,2,1]
  • cumulative entries by column: [1,3,4]

Signed Incidence Matrix

A signed incidence matrix is an incidence matrix where the sign of each nonzero entry is determined by the relative orientation of the two simplices corresponding to that row/column. (Closely related to discrete exterior calculus)

Half Edge Mesh

Split each edge into oppositely oriented half-edges.

struct HalfEdge{
  HalfEdge* twin;
  HalfEdge* next;
  Vertex* vertex;
  Edge* edge;
  Face* face;
}

// combine with he->twin to get full edge
struct Edge{
  HalfEdge* halfEdge;
};

// follow he->next until you return
struct Face{
  HalfEdge* halfEdge;
};

// look at he->twin->next
struct Vertex{
  HalfEdge* halfedge;
}

Defn Let $H$ be any set with an even number of elements, let $\rho: H \mapsto H$ be any permutation of H, and let $\eta : H \mapsto H$ be an involution without any fixed points, i.e $\eta \circ \eta = id$ and $\eta(h) \neq h ~ \forall h \in H$. Then, $(H, \rho, \eta)$ is a half edge mesh, the elements of $H$ are called half edges, the orbits of $\eta$ are edges, the orbits of $\rho$ are faces, and the orbits of $\rho \circ \eta$ are vertices. (Slides are wrong/follow different conventions)

($\eta$ is the twin and $\rho$ is the next operation.)

Fact: Every half edge mesh describes a compact oriented topological surface (without boundary).

Quad Mesh

Store sym(e), rot(e). Looks somewhat like delaunay?

Useful for dual complex. (Some isomorphism from mesh to a dual mesh)

a	b	c	d
Primal mesh	0-simplex (vertex)	1-simplex (edge)	2-simplex (tri)
Dual mesh	2-cell (hexagon)	1-cell (dual edge/rot(e))	0 cell (point)

Motivation: record measurements of flux through versus along elements.

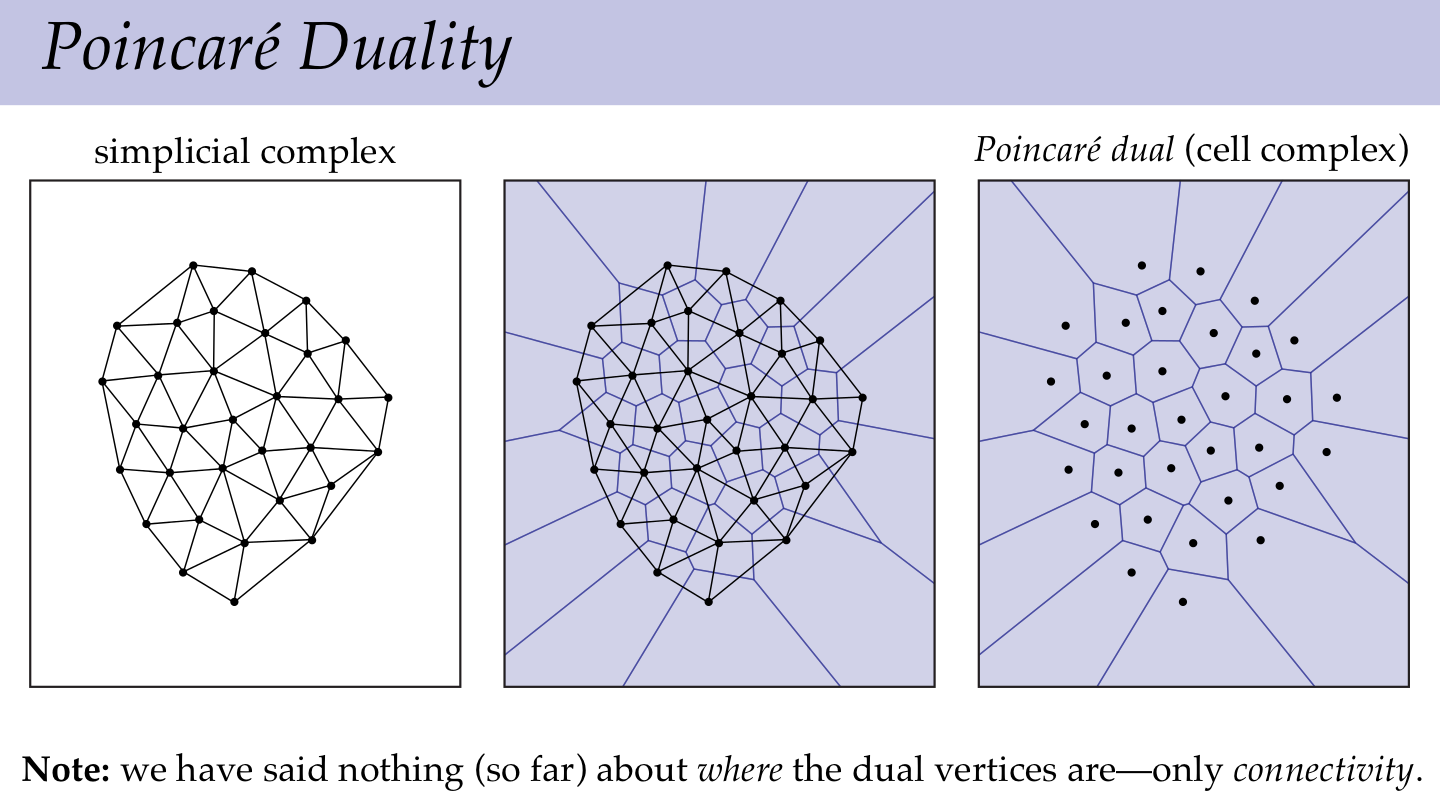
やっぱドロネーっぽいけど幾何については何も指定してない。

Reading 2

Lecture Notes Section 2.

基本的に講義内容と同じ。 pure k-simplicial complex なる概念の登場。 Every simplex $\sigma \in K$ is a face of a k-simplex. 的な感じ。

Pure k-subcomplex にはboundaryとinteriorという概念がある Boundary of $K'$ is the closure of the set of all simplices $\sigma$ that are proper faces of exactly one simplex of $K'$. The interior is $K' \backslash bd(K')$.